Central Limit Theorem Crack Torrent (Activation Code) Free For Windows
- lidograinuaba
- May 20, 2022
- 4 min read
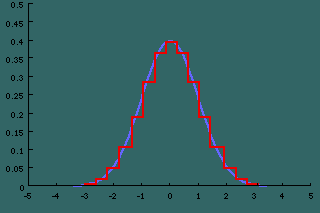
Central Limit Theorem Crack Full Product Key Free Download For Windows [2022] The Central Limit Theorem (CLT) states that the Central Limit Theorem (CLT) states that the sum of a large number of independent and identically distributed (IID) random variables drawn from a certain distribution converges to a Gaussian, with mean 0 and variance 1, under certain conditions. The Gaussian distribution is the most symmetric distribution; the average of many values can be approximated by the mean and the standard deviation of the distribution. There is a resemblance between the Central Limit Theorem and the Law of Large Numbers (LLN) that approximates the average of a large number of observations by the average of a sample. They can be used to calculate the average of a large number of observations. The Central Limit Theorem allows you to find the normal distribution of the sum of independent and identically distributed random variables. The Central Limit Theorem (CLT) can be stated as follows: If X1, X2, X3, …, XN are independent and identically distributed random variables having a common probability distribution and X = X1 + X2 + X3 + … + XN, then X has a normal distribution. For a detailed proof of the Central Limit Theorem, please visit: The Central Limit Theorem follows from the Law of Large Numbers, which states that if X1, X2, X3, …, XN are independent random variables drawn from the same probability distribution, the average of N such random variables also follows a normal distribution (the Central Limit Theorem is a special case of the Law of Large Numbers). These two results, together, lead to a practical method of calculating the properties of the sum of independent random variables. Uses of Central Limit Theorem: In practice, we often have data that we would like to analyze and where the data may have a non-normal distribution (for example, data that is not uniformly distributed), but where the central limit theorem is still applicable. The Central Limit Theorem is useful in such cases because it allows the derivation of statistical properties for large numbers of random variables, independent of their individual properties. Limitations of Central Limit Theorem: The Central Limit Theorem is only applicable when the random variables are "random" and do not depend on previous observations. For example, if your test questions were distributed among all students, then the test would be random, but the previous answers would not Central Limit Theorem Crack Free PC/Windows 1a423ce670 Central Limit Theorem With Registration Code The Source code is written in Java. It is divided into several packages. A Java applet is used to simulate random variables. The server code is distributed as source files to the Java class files. The client code is used to download, run and simulate the random variables. The CCLT is an application designed to illustrate the Central Limit Theorem for which it calculates the amount of times you need to throw a dice in order to get a sample of 4 heads equal to the 1 in 652,874 for a Poisson process. This application allows you to input a list of data values and at run-time calculate the standard deviation, the mean and the variance of the data set. There are two modes of operation: simulation mode and a full analytic mode. The simulator mode allows you to simulate the properties of a set of data in a separate window. The analytic mode allows you to generate output from the CCLT for the data sets you provide. Central Limit Theorem is an application for illustrating the Central Limit Theorem. Its purpose is to illustrate the Central Limit Theorem by simulation. It simulates the sum of n i.i.d. random variables (X1,..., Xn) and gives the following output: distribution of the central limit theorem by means of a graphic representation and the associated table containing the simulated data. You can either upload your own data file or use the simulator to input the data you wish to graphically represent. As I explain, a point is the center of a circle that is inscribed in a rectangle. Now use the work at the back of this book to finish the last two problems. I can remember the exact wording of the word of the problems. What is a Box-Muller transform? It is a mathematical transformation on a set of random variables that produces uniformly distributed random variables. The Box-Muller transform is widely used in finance and statistics. It is used to obtain standard normally distributed variables. The calculator is used to calculate the factorial of a number and the probability of a factorial number occurring. This is used in many different areas, such as in lottery games. The calculator is available for any number that is not a multiple of 3 or 5. Linear Programming: A solution of the problem described in this book on page 609 " A box packing problem " is presented. The linear program deals with finding the minimum cost for a set of objects to be packed into What's New In? System Requirements For Central Limit Theorem: All information provided is subject to change. Tablet: 1 GHz CPU or higher 2GB RAM or higher High-resolution screen Broadband Internet connection iOS: iOS 8.4 or higher iPhone or iPod touch with iOS 8.4 or higher Android: Android 2.2 or higher Other devices: Other operating systems or Internet browsers Minimum requirements: OS version: 7.0 Memory: 512MB Minimum requirements are not limited to the
Related links:








Comments